柱や梁のような棒状の材料(線材)は、
力が加えられた時の曲げの影響を無視できない。
力が加えられて曲がる際には、
材料の中で曲げられようとする力が生じている。
その力のことを曲げモーメントと呼び、
どの位置でどれぐらいの曲げモーメントが生じているか?
一眼でわかるグラフを曲げモーメント図と呼んでいる。
曲げモーメント図はM図とも呼ばれ、
このM図の読み解き方を理解すると、
曲げられる材の負担の様子をイメージしやすくなる。
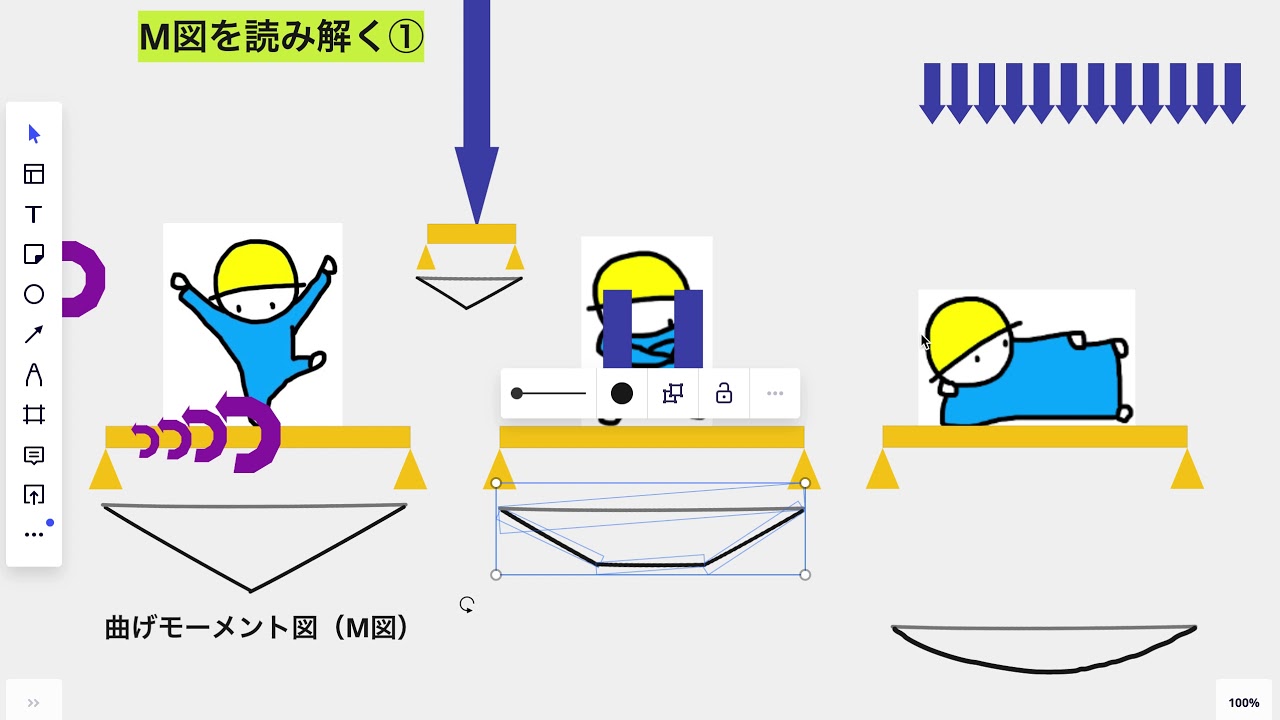
①単純梁の曲げモーメント図
中央1点に力が加わる場合、
2点に分散して加わる場合、
まんべんなく分布して加わる場合、
分けて加えるほど、曲げモーメントの最大値は小さくなる。
2段重ねた二重梁の曲げモーメントについて
上下の梁の曲げモーメントを合わせると
一本の梁の曲げモーメントと同じになる。
②骨組(ラーメン構造)の曲げモーメント図
鉛直荷重が加わる梁で、
単純梁と両端が固定された梁を比較する。
固定されることによって、
両端部で曲げモーメントに抵抗する。
それにより、
単純梁の曲げモーメントが引き上げられる形になり、
中央の曲げモーメントの最大値が小さくなる。
両端部が柱で固定されているラーメン構造の場合。
(ラーメン構造:接合部がしっかりと剛接合として固定されている構造)
梁の端部の曲げモーメントが柱にも伝わる。
それにより柱にも曲げモーメントが生じる。
③骨組に水平力が作用した時の曲げモーメント図
足元が固定された柱に水平力が作用した場合の
曲げモーメント図は、
片持梁に上から力が加わった場合と同じである。
それを2本並べてつなげると
片持梁2本の曲げモーメントが並んだような形になる。
柱の足元(柱脚)の固定度合いと
柱の頭(柱頭)の固定度合いを変えると、
梁の端部の曲げモーメントの大きさが変わる。
柱の留め方次第で、
柱脚と柱頭の曲げモーメントの大きさをコントロールできる。
梁の曲げモーメントもそれに連動するので、
柱の足元を支える基礎や梁のことも考えて、
どうするかを決定する。