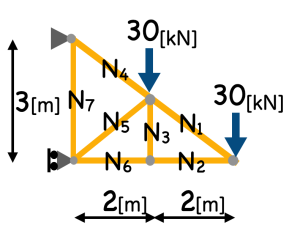
三角形のトラスの計算 その１ 節点法
ピン接合された部材で三角形を構成した構造はトラス構造と呼ばれている。
全体の形が三角形になっているトラスについて考える。
ナレーションを加えた動画はこちら→https://youtu.be/MjvP1YvRAIE
動画の補足説明
■大きな三角形のトラスの斜材の中間に荷重が作用すると
斜材には曲げモーメントが生じる。
■このとき、束には引張力が生じている。
■一つ一つの部材の断面力を求めるためには、
対象とする部材が接合されている節点を取り出して考える。
■その節点に接合されているすべての部材の力に関する力の釣合式を立てる。
■力の釣合式は直交する２方向の２つを立てることができる。
多くの場合、鉛直方向（縦）と水平方向（横）の釣合式を立てる。
■その釣合式を解けば、求めたい２つの断面力を計算することができる。
■力の釣合式を立てるときに、節点から出ていく向きの矢印を想定しておくと
その矢印の向きは引張力であることを意味しているので、
答えがプラスであれば引張力、マイナスであれば圧縮力であることを示す。
■一つの節点で接合される部材の断面力を求めることができれば、
その次の節点で同じように力の釣合式を立てて、同様に他の部材の断面力も求めることができる。
参考文献
ここで示した考え方が次の本に書かれています。
力学的なことを直感的に学べる良書です。
建築の絵本 建築構造のしくみ 第二版 力の流れとかたち
川口衞・阿部優・松谷宥彦・川崎一雄 著
ISBN：978-4-395-32015-8
2014年06月
彰国社のサイト https://www.shokokusha.co.jp/?p=820
演習
上の図の斜材の勾配は45度であるものとします。
建築では屋根の傾きは水平10に対して垂直に上がる寸法で表します。
10に対して4上がる傾きを4寸勾配と呼びます。
45度の傾きは水平10に対して垂直に10上がりますが、
この場合、10寸勾配とは呼ばずに矩（かね）勾配と呼びます。
三角形のトラスの計算 その2 図解法
トラスの断面力を求める方法の一つに図解法を呼ばれるものがあります。
節点に作用している力が釣り合っているとき、
力の矢印の長さを力の大きさに対応させて向きを正確に描くと、
そのすべての力の矢印は一周回って閉じた形になります。
その図を描くことによって、断面力を求めることができます。
ナレーションを加えた動画はこちら→https://youtu.be/n3sKiIOHrNo
動画の補足説明
■断面力を求めたい部材の節点を取り出して考える。
■節点に作用している力のうち、大きさと向きが分かっている力を描く。
■求めたい力の作用する方向を確認しながら、1周回って閉じた形を描く。
■連続していく形で一周回るようになる向きに矢印の矢を描く。
■元の節点の場所に、それぞれの矢印を戻すと、断面力の大きさが確認できる。
■元の節点の場所に矢印を戻したときに、
節点から出る矢印であれば引張、入る矢印であれば圧縮の力であると判断できる。
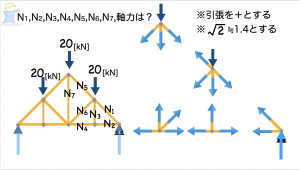
演習
図のトラスの断面力N1からN7まで、図解法で求めてください。
さらに左側の支持部分の反力も求めてください。
