片持梁 集中荷重
片持梁(cantilever)は、固定端でのみ支えられている。
もう一方の端部は自由端で、宙に浮いた状態である。
固定端にはどのような力が生じているか？その反力について考える。
https://youtu.be/bMUgi7Mvfx0
音読さんでナレーションを加えた動画はこちら→https://youtu.be/jkKAi0JofyY
ナレーションのない動画の補足
■上から下向きに加わる力と同じ大きさの力が反対向き（下から上向き）に生じている。
■上下方向の荷重と反力が同じ大きさで釣り合っていても、
作用する位置が異なるので、上下方向の力だけでは、梁は回転する。
■加わる力のことを荷重、固定端に生じている力を反力と呼ぶ。
■その回転を止めるために固定端には曲げモーメントも生じるものと捉える。
■固定端を中心に回転させようとする曲げモーメントの釣り合い式を立てる。
■曲げモーメントの大きさは、力の矢印の大きさと中心とする点から矢印の作用線までの距離を掛け算して求める。
■時計の針が動く右回りを＋として考えると
反対回りは−になる。
■計算した答えが−の場合は、もともと仮定した矢印と反対向きの力が生じていることになる。
解説
食堂でお盆を持つ手のことを考えてみる。
両手で両端を持つことが多いかもしれない。
お盆を持ちながら、片手で何かを取ろうとするとき、
片手だけでお盆を支えることになる。
この状態は、片持梁である。
お盆を持つ手でお盆の端をしっかり握る。
落ちないように支えるだけでなく、
お盆が傾かないように、手で掴んで曲げモーメントに抵抗している。
片持梁 分布荷重
固定端でのみ支えられている片持梁について、
たとえば自重のことを考慮する場合には、
分布荷重として作用しているものとして扱う。
分布荷重を集中荷重に置き換えて考えると、
集中荷重の計算と同様に、固定端の反力を求めることができる。
https://youtu.be/zAXlRACLPQA
音読さんでナレーションを加えた動画はこちら→https://youtu.be/iVpZ2DsUY4g
ナレーションのない動画の補足
■分布荷重は単位長さ（たとえば1m）あたりの力の大きさで示されている。
■等しく分布荷重が作用している場合には、
単位長さあたりの力に、分布荷重が加わっている部分の長さを掛け算すれば、
分布荷重の合計を求めることができる。
■計算した力の合計が集中荷重として作用しているものと置き換えて扱う。
■作用する点は、分布荷重の重心になる。
長方形であれば真ん中（全体の長さの半分）に置き換えた集中荷重が作用するものとして扱う。
■集中荷重に置き換えた後は、集中荷重と同様に計算をする。
解説
床の荷重が周辺の梁への加わり方を考えるとき、
分布荷重が当分布ではなく、三角形や台形の分布になる。
三角形の分布荷重を集中荷重に置き換えるときには、
合計は三角形の面積で計算する。
置き換えた集中荷重が作用する点は三角形の重心になる。
そのため、中央ではなく1：２になる位置に作用するものと考える。
片持梁 集中荷重 M図
片持梁に集中荷重が作用した時、梁の途中に生じている力（断面力）を求める。
https://youtu.be/XOPz_4_LEzY
VOICEVOX:琴詠ニアのナレーションを加えた動画はこちら→https://youtu.be/jO7FVwDfD5U
ナレーションのない動画の補足
■梁の途中に生じている力を断面力と呼ぶ。
■断面力を求めるためには、知りたい箇所で仮に切断して考える。
■反力を求める手順と同じように、仮に切断した箇所に想定した断面力も考慮して、
力の釣り合い式を立てる。
■力の釣り合い式を解けば断面力を求めることができる。
■材料の長さを横軸にして、断面力の大きさを示すグラフを描くことができる。
■曲げモーメントの大きさを示すグラフを曲げモーメント図と呼ぶ。
解説
曲げモーメント図を上に描くか？下に描くか？
日本の建築の分野では、
材料が軸方向に引っ張られる側に描くことにしている。
このルールに従って描くことにしておくと、
曲げモーメント図を見ただけで、どちら側が引っ張られているかが分かる。
曲げモーメント図は、曲がる力の負担の大きさを示している。
負担が大きな部分の断面を大きくする場合、
梁の見た目が、曲げモーメント図の形に応じた形になる。
片持梁 分布荷重 M図
分布荷重が作用する片持梁の途中に生じる力の計算方法を学ぶ。
https://youtu.be/ntEVeGkFwAc
VOICEVOX:琴詠ニアのナレーションを加えた動画はこちら→https://youtu.be/Hcr2EJekBq4
ナレーションのない動画の補足
■断面力を知りたい箇所で仮に切断して考える。
■求めたい断面力も含めて力の釣り合い式を立てる。
■計算しようとしている部分すべてに分布荷重が作用している。
その分布荷重を１つの集中荷重に置き換える。
■等分布荷重の場合には、計算しようとしている部分の中央に置き換えた集中荷重が作用するものとみなす。
■それぞれの箇所で計算した断面力の大きさをつなぐと
断面力の大きさを示すグラフを描くことができる。
■分布荷重の曲げモーメントは、
長さを掛け算して求めることになるので２次関数になる。
そのため、曲げモーメント図は曲線になる。
解説
片持梁として描かれた図の多くは、梁が水平である。
しかし、たとえば、
地面から生えている樹木は、垂直に立てられた片持梁である。
横から受ける風に対して、片持梁として抵抗している。
改めて、モーメント図と重ね合わせて樹木の姿を眺めると、
これまでとは違う見え方がするかもしれない。
重ね合わせの原理
片持梁を例にして、重ね合わせの原理について考える。
集中荷重が作用すると同時に分布荷重も作用しているとき、
それぞれを別々に考えて、答えを足し合わせても、
両方の荷重を足し合わせた式から答えを得ても、
その答えは同じになる。
https://youtu.be/pohgN12LSak
VOICEVOX:琴詠ニアのナレーションを加えた動画はこちら→https://youtu.be/ZfSs84CRdzU
ナレーションのない動画の補足
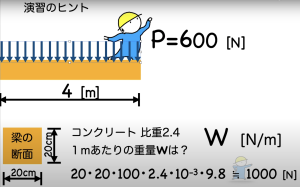
■片持梁の自重は分布荷重が作用しているものと考えて扱う。
■1mあたりの重量が分かれば良いので、断面積に長さ100cmを掛けて、さらに比重を掛ければ
1mあたりの重量がわかる。
■gをkgに換算して、9.8を掛けて力の単位Nにしておく。
■分布荷重のみ作用したものとして計算できる。
■集中荷重のみが作用したものとして計算もできる。
■分布荷重、集中荷重が同時に作用しているので実際の値は、２つを足したものとなる。
■最初から２つとも考慮した式を立てて計算しても、２つを足したものと同じ答えになる。
演習
動画で示した片持梁の例で端部の曲げモーメントの値を求めてみよう。
https://youtu.be/tKYYd_FJf5c 演習問題のヒント